[Algorithm] Shortest path(최단 경로)

최단 경로

• 최단 경로 알고리즘은 가장 짧은 경로를 찾는 알고리즘을 의미
• 다양한 문제 상황
  • 한 지점에서 다른 모든 지점까지의 최단 경로 + 음의 간선 → 벨만-포드 알고리즘
  • 한 지점에서 다른 모든 지점까지의 최단 경로 → 다익스트라 알고리즘
  • 모든 지점에서 다른 모든 지점까지의 최단 경로 → 플로이드 워셜 알고리즘

• 말 그대로 가장 짧은 경로를 찾는 알고리즘이다. (ex. 길찾기 문제)
• 최단 경로 문제는 보통 그래프를 이용해 표현하는데 각 지점은 그래프에서 노드로 표현되고 노드 간 연결된 선분은 간선으로 표현된다. 

Dijkstra Algorithm 

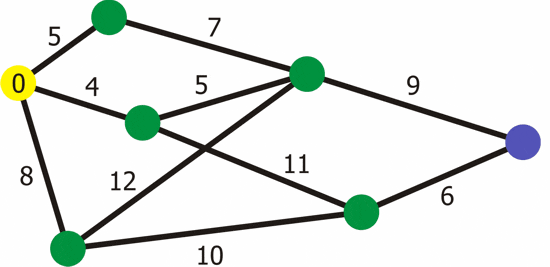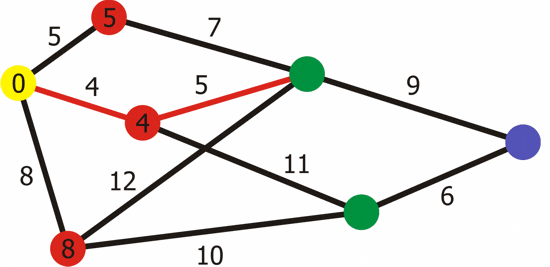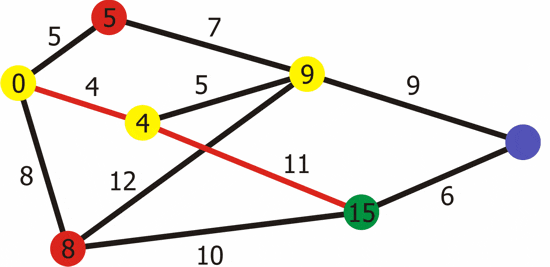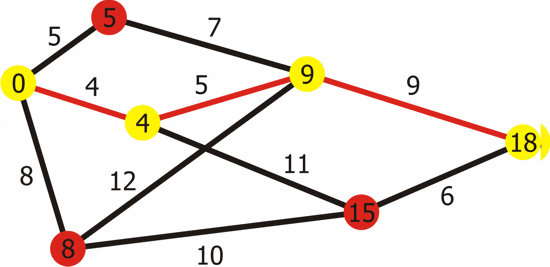
• 다익스트라는 그래프에서 양의 가중치가 있는 한 노드에서 모든 경로까지의 최단 경로를 찾을 때 사용한다. 
• 다익스트라 알고리즘은 기본적으로 그리디 알고리즘으로 분류된다. → 매번 가장 비용이 적은 노드를 선택해서 임의의 과정을 반복하기 때문이다. 
• 다익스트라 알고리즘은 간선이 E, 노드가 V개일 때, O(ElogV)의 시간 복잡도를 가진다. 
• 다익스트라 알고리즘은 방문하지 않은 노드 중에서 최단거리가 가장 짧은 노드를 선택하기 위해 매 단계마다 1차원 리스트의 모든 원소를 순차탐색한다. 
•  다익스트라는 heap 자료구조 기반의 Primary Queue를사용한다. 우선순위 큐을 사용하면 특정 노드까지 최단 거리에 대한 정보를 힙에 담아서 처리하므로 출발 노드로부터 가장 거리가 짧은 노드를 빠르게 찾을 수 있다
• 우선순위 큐를 사용할 때 (가중치, 노드) 순으로 삽입한다. 최소 힙의 특성으로 첫번째 원소 기준으로 정렬이 되기 때문에 시간적인 측면에서 이점을 볼 수 있다.
• 다익스트라 알고리즘은 반복문으로 구현할 수 있지만 효율이 매우 떨어지기 때문에 이해용으로만 알고 있자

# 다익스트라 - 반복문
# graph 초기화
# 출발 노드 확인
# 최단 경로 리스트 초기화
# 방문하지 않은 노드 중에서 최단 거리가 짧은 노드 선택
# 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 갱신 반복
import sys
input = sys.stdin.readline

n,m = map(int,input().split())
start = int(input())
graph = [[] for _ in range(n+1)]
visited = [False] * (n+1)
distance = [1e9] * (n+1)

for i in range(m) :
  a,b,c = map(int,input().split())
  graph[a].append((b,c))

def dijkstra(start) :
  distance[start] = 0
  visited[start] = True
  for i in graph[start] :
    distance[i[0]] = i[1]
  
  for i in range(n-1) :
    min_val = 1e9
    idx = 0
    for j in range(1,n+1) :
      if distance[j] < min_val and not visited[j] :
        min_val = distance[j]
        idx = j
      visited[idx] =  True
      for k in graph[idx] :
        cost = distance[idx] + k[1]
        if cost < distance[k[0]] :
          distance[k[0]] = cost

다익스트라 알고리즘은 다음과 같은 순서로 표현할 수 있다

1. 출발 노드를 설정 한 후, 출발 노드에서 각 노드의 최단 거리를 저장할 배열을 무한대로 초기화
2. 출발 노드에서 최단 거리를 계산하고 출발 노드의 최단 거리를 0으로 설정
3. 현재 노드에서 방문하지 않은 이웃 노드에 방문한 뒤 최단거리를 계산
4. 기존의 거리보다 짧은 경우 최단 거리를 업데이트
5. 모든 노드를 방문할 때 2번 과정을 반복

# 향상된 dijkstra
# ※ 무조건 가중치,노드 순으로 우선순위 큐를 만들어야 한다. 안그러면 시간초과 날수도 있다.
import sys, heapq
input = sys.stdin.readline

def dijkstra(graph,start,v) :               # 그래프 , 시작노드, 간선수
    dist = [1e9] * v 
    dist[start] = 0
    pq = [(0,start)]                        # 우선 순위 큐(가중치, 시작 노드)

    while pq :
        current_dist, u =  heapq.heappop(pq)    # 노드 u에 연결된 모든 인접 노드(가중치, 연결 노드)들을 검사
        										
        if current_dist > dist[u] :
            continue
        
        for weight, v in graph[u] :             # 노드 u에 연결된 모든 인접노드의 가중치 검사
            distance = current_dist + weight
            
            if distance < dist[v] :             # 새로운 최단 경로를 발견하면 dist를 갱신하고 우선순위 큐에 추가 
                dist[v] = distance
                heapq.heappush(pq,(distance,v))
    return dist
                
V,E = map(int,input().split())              # 간선 , 정점
K = int(input())                            # 시작 노드
graph = [[] for _ in range(V)]
for _ in range(E) :
    u,v,w = map(int,input().split())        
    graph[u-1].append((w,v-1))                # 시작노드 - (무게, 간선)
    
dist = dijkstra(graph,K-1,V)

for d in dist :
    if d == 1e9 :
        print("INF")
    else :
        print(d)

 

다익스트라 알고리즘
1. primary queue (우선순위 큐) 사용
2. primary queue에 append 할 때, (가중치, 노드)로 삽입
3. 한 지점에 대한 최단거리를 구할 때 사용

Floyd-Warshall Algorithm

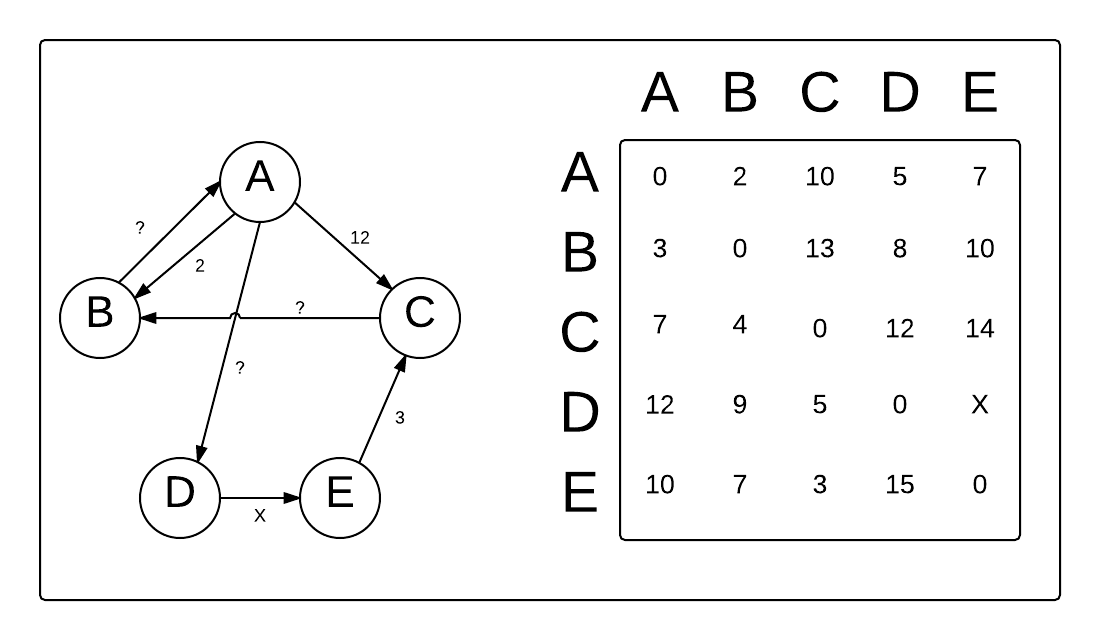
• 모든 지점에서 다른 모든 지점까지의 최단 경로를 구할 수 있다
• 인접행렬을 사용하여 모든 정점간의 거리를 계산
• 세 개의 중첩된 반목문을 통해 모든 정점 쌍에 대한 연산 수행
• 시간 복잡도: O(V^3)
• 공간 복잡도: O(V^2)

모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우에 사용할 수 있는 알고리즘이다. 플로이드-워셜 알고리즘의 시간복잡도는 O(N^3)이다.  점화식으로 표현하면 다음과 같다.

INF = int(1e9)

n = int(input())
m = int(input())
graph = [[INF] * (n+1) for _ in range(n+1)]

for a in range(1,n+1) :
  for b in range(1,n+1) :
    if a == b :
      graph[a][b] = 0

for _ in range(m) :
  a,b,c = map(int,input().split())
  graph[a][b] = c

for k in range(1,n+1) :
  for a in range(1,n+1) :
    for b in range(1,n+1) :
      graph[a][b] = min(graph[a][b],graph[a][k] + graph[k][b])


for a in range(1,n+1) :
  for b in range(1,n+1) :
    if graph[a][b] == INF:
      print("INFINITY",end=" ")
    else :
      print(graph[a][b],end=" ")
  print()

플로이드 워셜 알고리즘을 파이썬으로 구현하기 위해서는 다음과 같은 순서로 진행하면 된다 노드의 개수를 n 간선의 개수를 M이라 가정해보자.

1. 노드의 개수와 간선의 개수를 입력받는다. + 무한(INF = int(1e9)) 선언

2. graph의 각 값을 INF로 선언하고 2차원 배열 (n+1) * (n+1)로 선언해준다.

3. 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화한다. 2 중 for 문을 사용한다.

행 / 열	..	n
..	0	..
n	..	0

 

for a in range(1,n+1) :
	for b in range(1,n+1) :
    	if a == b:
        	graph[a][b] = 0

4. 각 간선에 대한 정보를 입력 받아 , 그 값으로 초기화 한다.

for _ in range(m) :
	a,b,c = map(int,input().split())
    	graph[a][b] = c

5. 플로이드_워셜 점화식에 따라 최소 거리를 반환한다. 3중 for 문을 사용한다.

for k in range(1,n+1) :
	for a in range(1,n+1):
    		for b in range(1,n+1):
        		graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b])

6. 수행 결과를 출력한다.

for a in range(1,n+1):
	for b in range(1,n+1):
            if graph[a][b] == INF :
            	print("INFINTIY",end=" ")
            else:
                print(graph[a][b],end=" ")
    print()

 

플로이드-워셜 알고리즘
1. 모든 지점에 대한 최단 거리를 알고 싶을 때 사용
2. 3중 for 문 사용
3. 점화식 : min(arr[i][j], arr[i][k] + arr[k][j])

Bellman-Ford Algorithm

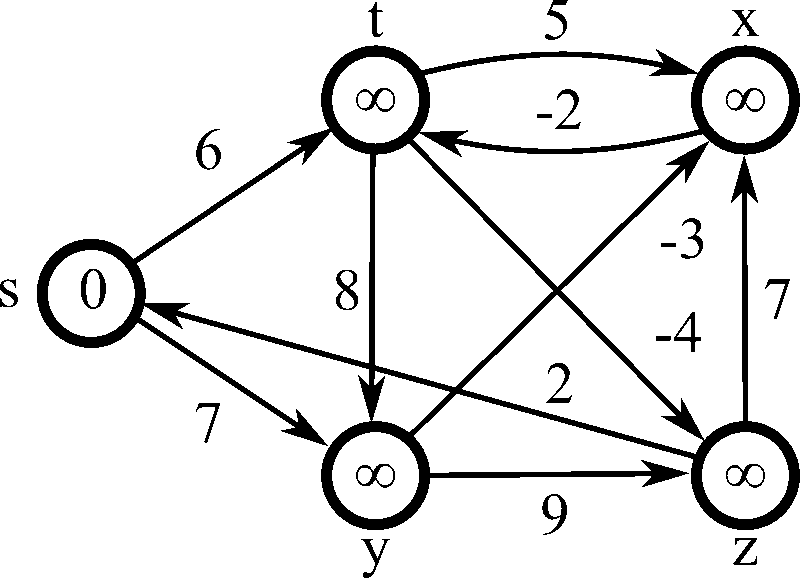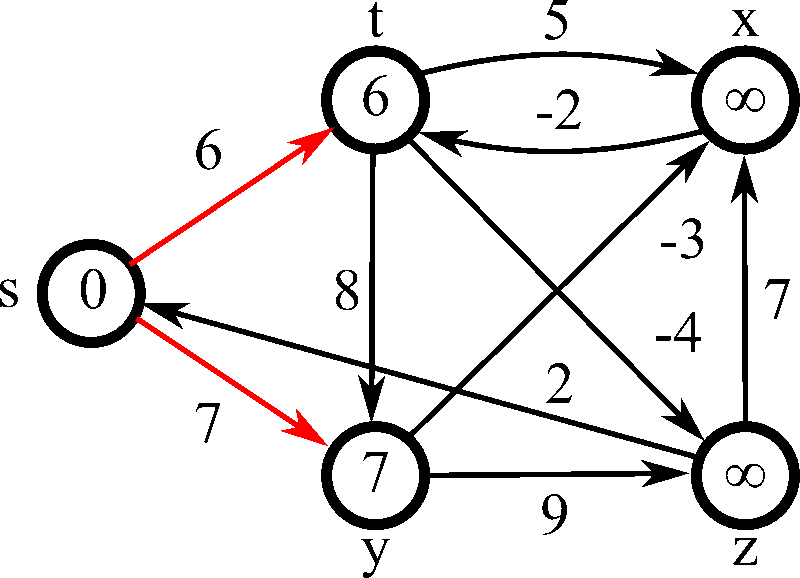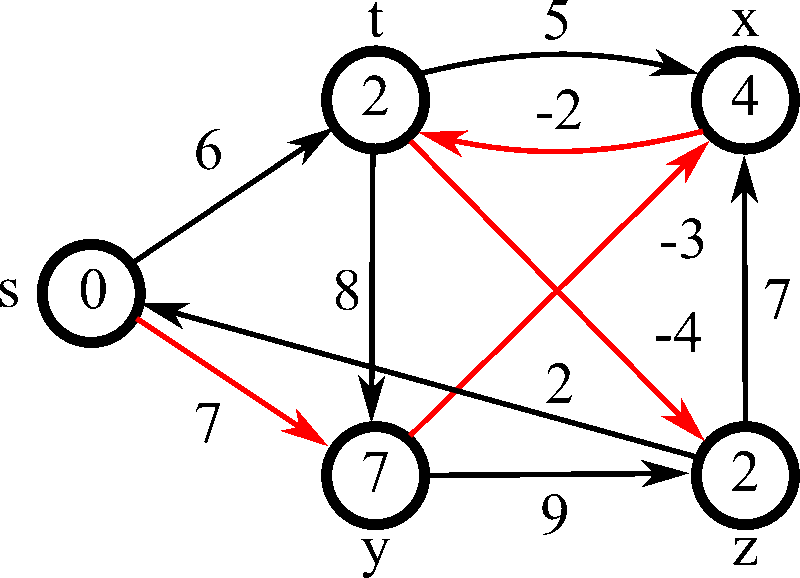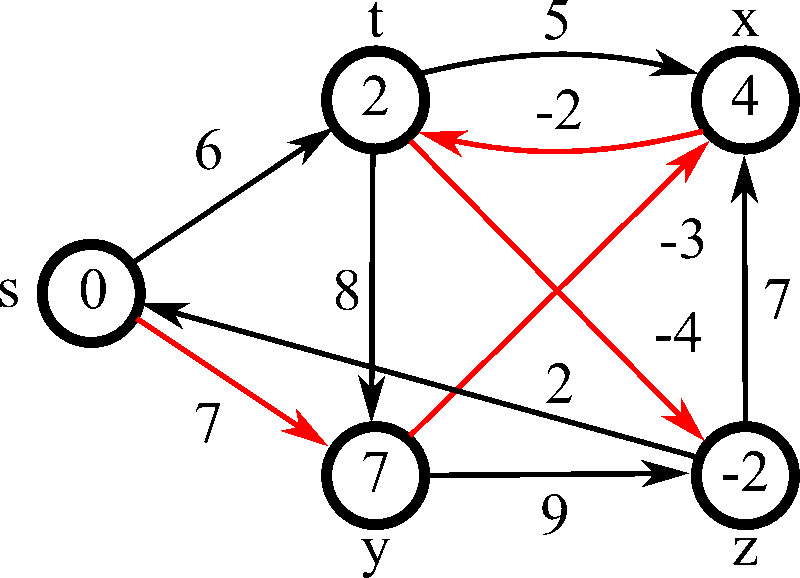
• 2차 for문을 순회하며 매 단계마다 모든 간선을 전부 확인하면서 노드 간의 최단 거리를 구한다
• 음수 간선이 있어도 최적의 해를 찾을 수 있다.
• 시간복잡도: O(VE)
• 동작방식
  1. 출발 노드를 설정
  2. 최단 거리 테이블을 초기화
  3. 다음의 과정을 V-1번 반복
  4. 모든 간선을 확인
  5. 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신

class Edge:
    def __init__(self, u, v, weight):
        self.u = u
        self.v = v
        self.weight = weight

def bellman_ford(edges, V, E, start):
    dist = [float('inf')] * V
    dist[start] = 0

    for _ in range(V - 1):
        for edge in edges:
            if dist[edge.u] != float('inf') and dist[edge.u] + edge.weight < dist[edge.v]:	# 2차 for문을 통해 값을 최신화
                dist[edge.v] = dist[edge.u] + edge.weight

    for edge in edges:
        if dist[edge.u] != float('inf') and dist[edge.u] + edge.weight < dist[edge.v]:		# 사이클을 돌 때마다 값이 계속 작아진다(음의 Cycle 존재)
            print("음의 가중치 사이클 존재!")
            return None  # Or handle the negative cycle case as needed

    return dist

def main():
    V = int(input())
    E = int(input())
    start = int(input()) - 1

    edges = []
    for _ in range(E):
        u, v, weight = map(int, input().split())
        edges.append(Edge(u - 1, v - 1, weight))

    dist = bellman_ford(edges, V, E, start)
    
    if dist is not None:
        for d in dist:
            if d == float('inf'):
                print("INF")
            else:
                print(d)

if __name__ == "__main__":
    main()

참고 : 이것이 취업을 위한 코딩 테스트다 with 파이썬 )

https://github.com/ndb796/python-for-coding-test

GitHub - ndb796/python-for-coding-test: [한빛미디어] "이것이 취업을 위한 코딩 테스트다 with 파이썬" 전체