| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- sql
- Algorithm
- JPA
- 자료구조
- DB
- 코딩테스트준비
- js
- 99클럽 #코딩테스트준비 #개발자취업 #항해99 #til
- 공개키 암호화
- 위상정렬
- 99클럽
- jsp
- 코테
- javascript
- 개발자취업
- 항해99
- dbms
- Sort
- generic class
- python
- spring
- BFS
- Java
- 알고리즘
- 정렬
- 크루스칼
- 가상컴퓨팅
- til
- 자바의정석
- 코딩테스트
- Today
- Total
PLOD
[Algorithm] 동적계획법(Dynamic Programming : DP) 본문
[Algorithm] 동적계획법(Dynamic Programming : DP)
훌룽이 2023. 7. 6. 15:01동적계획법
컴퓨터는 굉장히 빠른 연산 속도를 장점으로 갖고 있기 때문에 인간이 풀기엔 오래걸리는 문제라도 컴퓨터로는 금방 답을 얻을 수 있다. 이 특징이 가장 두드러지는 방법이 완전탐색이다. 완전탐색은 범위가 작을 때는 시간,공간적으로는 괜찮았지만 범위가 10000000000 이상이라면 코딩테스트에서 시간 , 메모리 초과가 발생한다. 그래서 더 효율적인 알고리즘을 사용해서 풀어야 하는데 그 방법은 동적 계획법이다.

예를 들면 , 6번째 피보나치 수를 구하려면 5번째와 4번째가 필요하다 5번째를 구하기 위해서는 4번째와 3번째가 필요하고... 이렇게 계속 반복하다 보면 0번째와 1번째 까지 오게 된다 .
이를 가지고 2번째 피보나치 수를 구할 수 있고 연쇄적으로 6번째 피보나치 수를 구할 수 있다.
피보나치 수열을 구현할 때 , 재귀적 방법을 사용하면 f(n)에서 n이 커질 수록 시간이 기하급수적으로 커진다.
일반적으로 피보나치 수열의 시간복잡도는 O(2^n)이다. 그림을 보면 f(6)을 반환하는데 f(2)가 4번이나 호출되는 것을 볼 수 있다. 이렇게 불필요한 호출만 줄여도 수행시간을 줄일 수 있다.

동적계획법 구성
- 문제 분할: 하나의 문제를 작은 하위 문제로 나누어 해결
- 중복 계산 방지: 이전 계산 결과를 저장하여 동일한 계산을 반복하지 않음
- 최적 부분 구조: 문제의 최적 해가 하위 문제의 최적 해로 구성될 수 있는 구조
Memoization : 메모이제이션
피보나치 수열 구현에서 , 중복 호출 문제를 해결하는 방법으로 메모이제이션 방법이 있다. 메모이제이션은 다이나믹 프로그래밍(DP)를 구현하는 방법 중 한 종류로, 한 번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법을 의미한다. 다음과 같이 fibo(99) 같은 99번째 피보나치 수열을 구하는 문제에도 런타임에러가 나지 않고 출력하는 것을 볼 수 있다. 메모이제이션은 DP문제를 풀 때 반드시 필요한 필수 개념이다. 메모이제이션을 사용하지 않으면 대부분 시간 초과가 발생할 것이다
# 하향식(Top-Down)
# 큰 문제를 해결하는 과정에서 하위 문제를 재귀적으로 호출
# **`메모이제이션(Memoization)`** 방법을 통해 중복계산 피함
d = [0] * 100
def fibo(x) :
if x == 1 or x == 2 :
return 1
if d[x] != 0 :
return d[x] # 메모이제이션 - 값을 재호출한다.
d[x] = fibo(x-2) + fibo(x-1)
return d[x]
print(fibo(99))처음에 -1로 초기화하고, f(n)을 호출할 때 이미 구한 적이 있는 적이 있는 부분 문제인지 살펴 본다. cache에 -1이 아닌 어떤 다른 수가 있다면, 이 전에 f(n)가 호출되어 답을 저장 했다는 의미일테니, 이 경우에는 바로 구해 놨던 답을 반환하고 끝낸다. -1이 들어있다면 처음 호출되었다는 의미이므로 부분 문제의 답을 구해서 cache에 넣는다.
Tabulation : 타뷸레이션
피보나치 수를 구하는 문제는 재귀함수 외에 반복문으로도 구할 수 있다. 이때는 작은 수부터 구하게 되며 전부 구해서 저장해 두는 것을 타뷸레이션이라고 한다. 다음은 타뷸레이션 기법을 사용하여 36번째 피보나치 수를 구하는 파이썬 코드이다.
# 상향식(Bottom-Up)
# 하위 문제를 문저 해결하고 그 결과를 이용해 상위 문제 해결
# 반복문을 활용한 구현하며, **`타뷸레이션(Tabulation)`** 이라고 칭함
f = [-1] * 37
for i in range(37) :
f[i] = i if i < 2 else f[i-1] + f[i-2]
print(f[36])DP(Dynamic Programming : 동적계획법)
DP는 앞서 메모이제이션 기법을 사용하여 큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘이다. 다이나믹 프로그래밍이란 큰 문제를 작게 나누고 , 같은 문제라면 한번씩만 풀어 문제를 효율적으로 해결해나가는 알고리즘 기법이다. 다이나믹 프로그래밍은 재귀 방식을 사용하는 Top-down 방식과 반복문을 사용하여 문제를 해결해나가는 Bottom-up 방식이 있다.
| 구분 | Top-down | Bottom-up |
| 구현 | 재귀 | 반복문 |
| 장점 | 직관적이라 코드 가독성이 좋음 | 시간과 메모리를 좀 더 아낄 수 있음 |
| 단점 | 재귀함수를 많이 호출하여 느릴 수 있음 | DP 테이블을 채워 나가는 순서를 알아야 함 |
ex) baekjoon - 1463
https://www.acmicpc.net/problem/1463
1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
tabulation
d = [0] * 300001
N = int(input())
for i in range(2,N+1) :
d[i] = d[i-1] + 1
if i % 2 == 0 :
d[i] = min(d[i],d[i//2]+1)
if i % 3 == 0 :
d[i] = min(d[i],d[i//3]+1)
print(d[N])memoization
import sys
sys.setrecursionlimit(10**6)
INF = 987654321
N = int(input())
cache = [INF] * (N+1)
cache[1] = 0
def dp(x) :
if cache[x] != INF :
return cache[x]
if x % 6 == 0 :
cache[x] = min(dp(x // 3),dp(x // 2)) + 1
elif x % 3 == 0:
cache[x] = min(dp(x // 3),dp(x - 1)) + 1
elif x % 2 == 0 :
cache[x] = min(dp(x // 2), dp(x - 1)) + 1
else :
cache[x] = dp(x - 1) + 1
return cache[x]
print(dp(N))Prefix_Sum : 누적합
누적합은 0 부터 인덱스 i 까지의 합을 누적하여 리스트에 저장하는 것을 의미한다. 누적합을 사용하면 구해야 할 범위의 합이 클 때 빠르게 계산 할 수 있다. 예를 들면, 크기가 N인 리스트에서 i 부터 j 까지의 합을 알고 싶을 때, 0 ~ j까지의 합과 0 ~ i까지의 합의 차를 O(N)의 시간 안에 구할 수 있다.
ex) baekjoon - 11659
https://www.acmicpc.net/problem/11659
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net
import sys
input = sys.stdin.readline
N,M = map(int,input().split())
num = list(map(int,input().split()))
num_sum = [0]
temp = 0
for i in num:
temp += i
num_sum.append(temp)
for _ in range(M) :
i,j = map(int,input().split())
print(num_sum[j] - num_sum[i-1])가장 긴 증가하는 부분 수열 : LIS.Longest Increasing Subsequence

다이나믹 프로그래밍 문제의 전형적인 아이디어인 LIS 문제 이다. 가장 긴 증가하는 부분 수열 문제란 하나의 수열이 주어졌을 때 값들이 증가하는 형태의 가장 긴 부분 수열을 찾는 문제이다. 예를 들어 리스트 {10,20,10,30,20,50} 이때 가장 긴 증가하는 부분 수열은 {10,20,30,50} 이 될 것이다. d[i] = array[i]를 마지막 원소로 가지는 부분 수열의 최대 길이 라고 정의하면, 가장 긴 부분 수열을 계산하는 점화식은 다음과 같다.
모든 0 <= j < i 에 대하여, d[i] = max(d[i], d[j] + 1) if arr[j] < arr[i]
이 점화식을 코드로 구현하면 다음과 같다.
n = int(input()) # 리스트의 크기인 n을 입력받는다
arr = list(map(int,input().split())) # n크기의 리스트 원소를 입력
d = [1] * n
for i in range(n) :
for j in range(i) :
if arr[i] > arr[j] :
d[i] = max(d[i],d[j]+1) # LIS 점화식
print(max(d))
ex) baekjoon - 18353
https://www.acmicpc.net/problem/18353
18353번: 병사 배치하기
첫째 줄에 N이 주어진다. (1 ≤ N ≤ 2,000) 둘째 줄에 각 병사의 전투력이 공백을 기준으로 구분되어 차례대로 주어진다. 각 병사의 전투력은 10,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
import sys
input = sys.stdin.readline
n = int(input())
power = list(map(int,input().split()))
power.reverse()
d = [1] * (n)
for i in range(1,n) :
for j in range(0,i) :
if power[j] < power[i] :
d[i] = max(d[i],d[j]+1)
print(n-max(d))배낭 문제(knapsack problem)
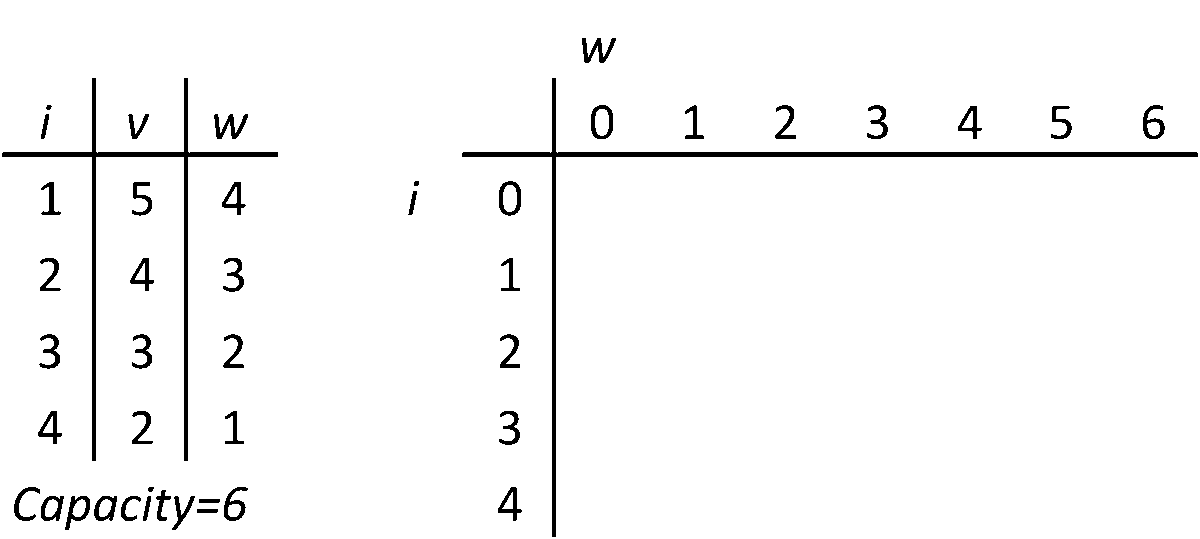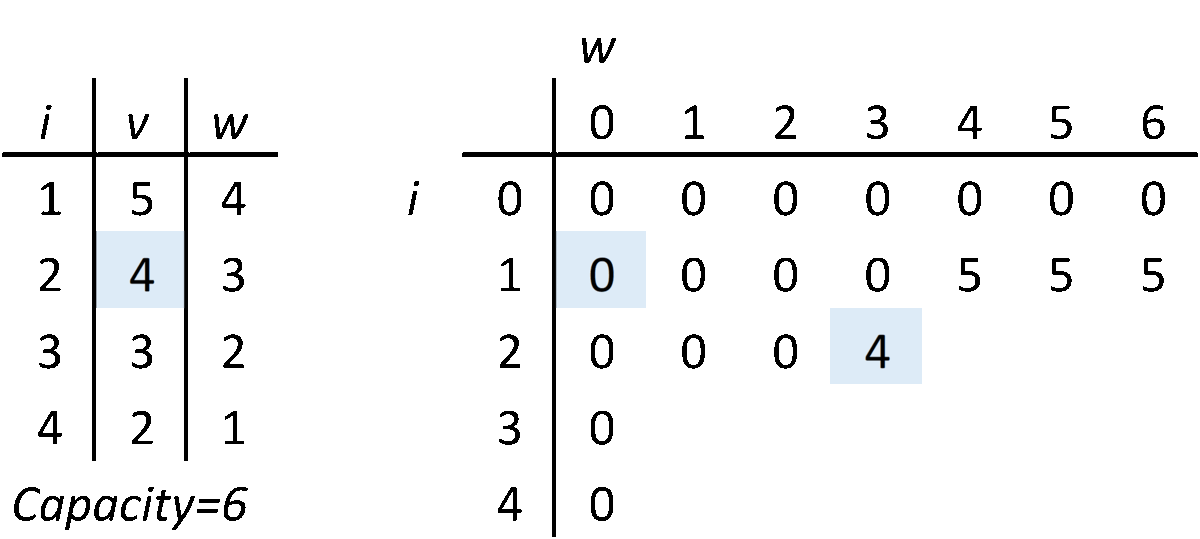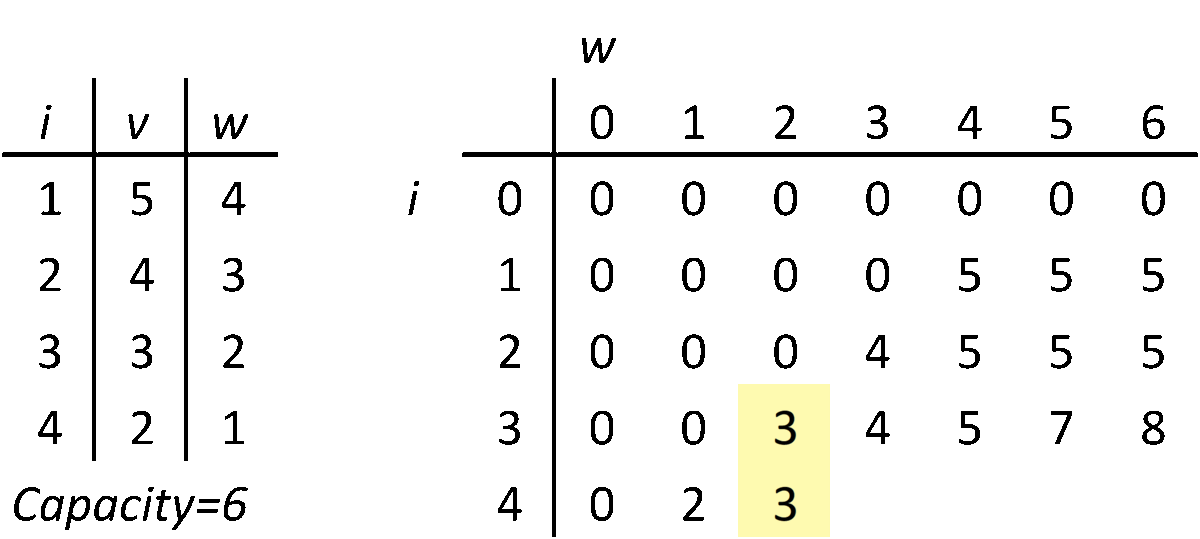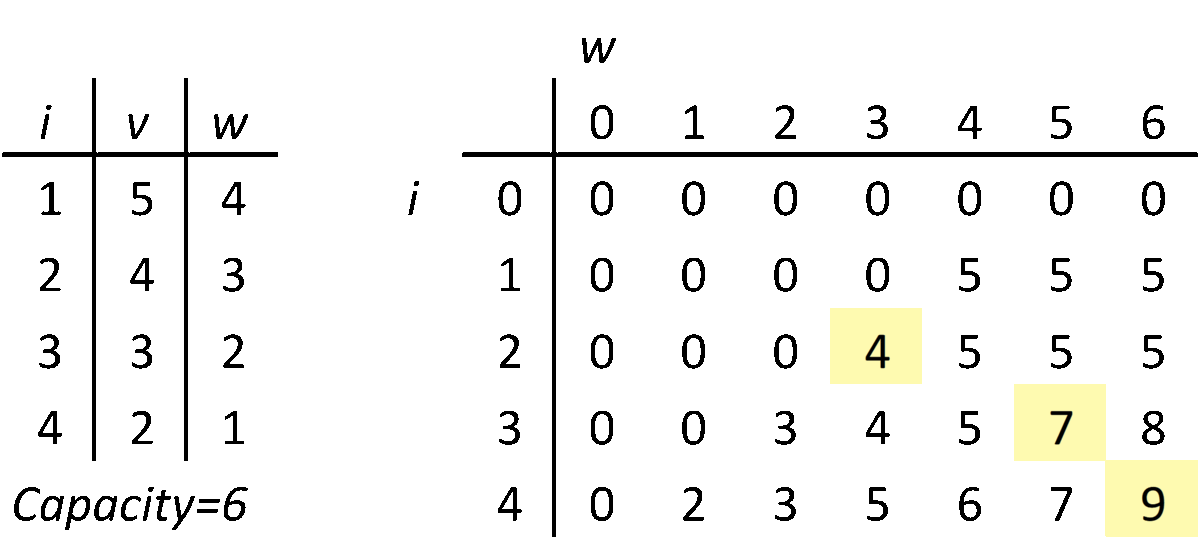
배낭에 담을 수 있는 무게의 최댓값(W)이 정해져 있고 , 일전한 가치의 무게가 정해진 짐들을 배낭에 담을 때, 가치의 합이 최대가 되는 조합을 찾는 알고리즘이다. 배낭 문제는 다이나믹 프로그래밍 이라는 방법을 쓰는 기본적인 문제로 알려져 있다. 배낭 문제에서 집합 A를 n개의 보석들 중에 최적으로 고른 부분집합이라고 가정하면
1. 집합 A가 n 번째 보석을 포함하고 있지 않다면, A는 n번째 보석을 뺀 나머지 n-1개의 보석들 중에서 최적으로 고른 부분 집합과 같다
→ dp [K+1][W] = dp [K][W]
2. 집합 A가 n번째 보석을 포함하고 있다면 A에 속한 보석들의 총 가격은 n-1개의 보석들 중에서 최적으로 고른 가격의 합에다가 보석 n의 가격을 더한 것과 같다(n 번째 보석을 넣었을 때 배낭이 터지지 않아야 한다.)
→ dp [K][W] = max(dp [K-1][W], K가치 + dp [K-1][W-K무게])

i번째 보석이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로 i번째 보석을 뺀 i-1개의 보석들을 가지고 구한 전 단계의 최적값을 그대로 가져온다. 그렇지 않은 경우 i 번째 보석을 위해 i번째 보석만큼의 무게를 비웠을 때의 최적값에 i번째 보석의 가격을 더한 값 이나 i-1개의 보석들을 가지고 구한 전 단계의 최적값 중 큰 것을 선택한다. P라는 2차원 리스트를 채워나가면서, 필요한 경우 앞에서 계산했던 다른 칸의 값을 이용해서 다음 칸의 값을 계산한다.
https://www.acmicpc.net/problem/3067
3067번: Coins
우리나라 화폐단위, 특히 동전에는 1원, 5원, 10원, 50원, 100원, 500원이 있다. 이 동전들로는 모든 정수의 금액을 만들 수 있으며 그 방법도 여러 가지가 있을 수 있다. 예를 들어 30원을 만들기 위해
www.acmicpc.net
import sys
input = sys.stdin.readline
n = int(input())
coin = list(map(int,input().split())) # n 경우의 동전
m = int(input())
d = [0] * (m+1) # m개의 dp 주머니 생성
d[0] = 0
for i in range(n) :
for j in range(coin[i], m+1) :
d[j] = min(d[j], d[j - coin[i]] + 1) # 배낭문제 점화식
print(d[m])
DP 문제 핵심
1. 점화식 설계 및 구현(중요)
2. 점화식 값을 저장할 배열 선언(메모이제이션 기법 사용시)
3. 초기 값을 잘 생각(ex. n <= 1 , 메모이제이션 + 타뷸레이션)
ex) baekjoon - 11726
https://www.acmicpc.net/problem/11726
11726번: 2×n 타일링
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.
www.acmicpc.net
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
n = int(input())
cache = [0] * (n+1)
def f(n) :
if cache[n] :
return cache[n]
if n == 1 :
cache[n] = 1
elif n == 2 :
cache[n] = 2
else :
cache[n] = (f(n-1) + f(n-2)) % 10007
return cache[n]
print(f(n))ex) baekjoon - 11727)
https://www.acmicpc.net/problem/11727
11727번: 2×n 타일링 2
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×17 직사각형을 채운 한가지 예이다.
www.acmicpc.net
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
d = [0] * 1001
def area(n) :
if n <= 1 :
return 1
if d[n] != 0 :
return d[n]
d[n] = (area(n-1) + (2 * area(n-2))) % 10007
return d[n]
n = int(input())
print(area(n))
ex) baekjoon-11055
https://www.acmicpc.net/problem/11055
11055번: 가장 큰 증가하는 부분 수열
수열 A가 주어졌을 때, 그 수열의 증가하는 부분 수열 중에서 합이 가장 큰 것을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {1, 100, 2, 50, 60, 3, 5, 6, 7, 8} 인 경우에 합이 가장 큰 증가하는
www.acmicpc.net
import sys
input = sys.stdin.readline
N = int(input())
dp = [i for i in range(N+1)]
for i in range(4,N+1):
for j in range(1,i) :
if i < j**2 :
break
if dp[i] > dp[i-(j**2)] + 1 :
dp[i] = dp[i-(j**2)] + 1
print(dp[N])참고 )
이것이 취업을 위한 코딩 테스트다 with 파이썬 )
https://github.com/ndb796/python-for-coding-test
GitHub - ndb796/python-for-coding-test: [한빛미디어] "이것이 취업을 위한 코딩 테스트다 with 파이썬" 전체
[한빛미디어] "이것이 취업을 위한 코딩 테스트다 with 파이썬" 전체 소스코드 저장소입니다. - GitHub - ndb796/python-for-coding-test: [한빛미디어] "이것이 취업을 위한 코딩 테스트다 with 파이썬" 전체 소
github.com
2023 한권으로 합격하는 취업 코딩테스트)
https://product.kyobobook.co.kr/detail/S000201209716
2023 한권으로 합격하는 취업 코딩테스트 | 컴공선배 - 교보문고
2023 한권으로 합격하는 취업 코딩테스트 | 코딩테스트 준비, 더 이상 막막하지 않다! 기업체에 개발자로 취직하려면 ‘코딩테스트’부터 합격해야 한다. 코딩테스트 출제 경향 분석부터 자료구
product.kyobobook.co.kr
https://gsmesie692.tistory.com/113?category=523232
Dynamic Programming: 배낭 채우기 문제 (Knapsack Problem)
도둑이 보석가게에 배낭을 메고 침입했다. 배낭의 최대 용량은 W이며, 이를 초과해서 보석을 담으면 배낭이 찢어질 것이다. 각 보석들의 무게와 가격은 알고 있다. 배낭이 찢어지지 않는 선에서
gsmesie692.tistory.com
https://howudong.tistory.com/106
배낭 문제(KnapSack Problem) 그림으로 쉽게 이해하기
배낭 알고리즘이란? 배낭 문제(Knapsack)는 n개의 물건과 배낭 있을 때, 각 물건에는 가치와 무게가 존재한다. 또한 각 물건은 1개씩만 있다. 배낭에는 담을 수 있는 최대 용량이 존재한다. 이러한
howudong.tistory.com
'computer science > Algorithm | Datastructure' 카테고리의 다른 글
| [Algorithm] Brute-force(완전탐색) , Backtracking(백트래킹) (0) | 2023.07.31 |
|---|---|
| [Algorithm] Shortest path(최단 경로) (0) | 2023.07.12 |
| [Algorithm] Search(탐색) (0) | 2023.07.05 |
| [Algorithm] sort(정렬 알고리즘) (0) | 2023.06.30 |
| [python] Simulation and Notation (1) | 2023.06.16 |




