Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- javascript
- DB
- Queue
- Java
- mybatis
- 공개키 암호화
- 코딩테스트준비
- sql
- 크루스칼
- 99클럽 #코딩테스트준비 #개발자취업 #항해99 #til
- dbms
- spring
- generic class
- 자료구조
- 암호학
- BFS
- 코딩테스트
- 알고리즘
- js
- Algorithm
- python
- jsp
- 가상컴퓨팅
- til
- 99클럽
- 자바의정석
- 항해99
- 개발자취업
- JPA
- 코테
Archives
- Today
- Total
PLOD
[crypto] Modular Arithmetic 본문
"x mod n"
Modulo Operation(모듈로 연산) : 어떤 한 숫자를 다른 숫자로 나눈 나머지(mod)를 구하는 연산으로, 나머지 연산이라고 한다. 모듈로 연산을 사용 하기 위해서는 나누는 수와
나누어지는 수가 서로 Relative Primality(서로소) 관계여야 한다.
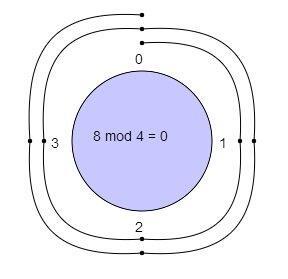
모듈로 연산을 사용한 Modular Arithmetic(Clock Arithmetic)은 공개키 암호화 알고리즘의 시초이다.
정수 X와 n 이 주어졌을때, x mod n 은 컴퓨터 연산에서 x % n 과 같다.
즉 , 모듈로 연산은 x를 n으로 나눈 나머지를 구하는 연산이다.
ex.1)
14 mod 3 = 2 mod 3(14 mod 3과 2 mod 3은 나머지가 같다)
ex.2)
-2 mod 6 = 4 mod 6( 6 - 2 = 4)
ex.3)
1/3 mod 7 = 5 mod 7
(3 * 1 = 3 => 3 mod 7 = 3
3 * 2 = 6 => 6 mod 7 = 6
3 * 3 = 9 => 9 mod 7 = 2
3* 4 = 12 => 12 mod 7 = 5
3 * 5 = 15 => 15 mod 7 = 1)
-> Euclidean Algorithm을 사용
* Totient Function (ϕ(n)) : 오일러 파이(피) 함수
: n 과 서로소인 1부터 n 까지 정수의 개수와 같다.
ex)
ϕ(6) = 2 (1,5)
ϕ(4) = 2(1,3)
ϕ(5) = 4(1,2,3,4)
ϕ(12) = 4(1,5,7,11)
ϕ(p) = p-1 일 때, p는 소수이다.
ϕ(p*q) = (p-1) * (q-1) 일때 p와 q는 소수이다.
'computer science > Cryptography' 카테고리의 다른 글
| [crypto] SSL/TLS (0) | 2022.12.08 |
|---|---|
| [crypto]Authentication Protocols (0) | 2022.12.07 |
| [crypto] Hash (0) | 2022.12.05 |
| [crypto]Diffie-‐Hellman (0) | 2022.12.05 |
| [crypto] Public Key Cryptography (1) | 2022.12.05 |
Comments




