Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 자바의정석
- python
- 개발자취업
- dbms
- sql
- 암호학
- javascript
- dfs
- 크루스칼
- generic class
- data structure
- 항해99
- Algorithm
- 자료구조
- 생성자
- spring
- 코딩테스트준비
- 알고리즘
- JPA
- DB
- 코테
- BFS
- 문자열
- js
- Java
- 공개키 암호화
- jsp
- 가상컴퓨팅
- Queue
- 코딩테스트
Archives
- Today
- Total
PLOD
[Python] graph(그래프) 와 tree(트리) 본문
Graph

- 그래프는 정점(데이터)과 간선(데이터 간의 거리)으로 이루어진 자료구조이다.
- 그래프는 BFS,DFS 같은 순회 알고리즘과 Djikstra 같은 최소경로알고리즘을 구현할 때 알아야 될 필수 자료구조이다.
- 그래프는 정점(vertex,node)와 노선인 간선(edge)으로 이루어져 있다.
- 그래프는 간선의 방향성을 기준으로 나뉜다.

- 그래프는 방향 그래프(Directed graph)와 무방향 그래프(Undirected graph : 양방향 그래프)가 있다.
- 그래프는 순환성을 기준으로 나눌 수도 있다.
- 순환 그래프와 비순환 그래프가 있다.
인접 행렬을 통해서 그래프를 만들기
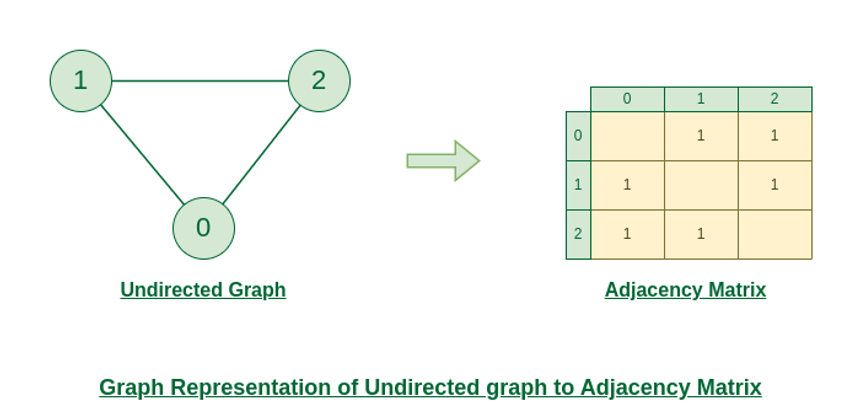
인접 행렬
- 2차원 배열을 사용하여 그래프의 정점들 간의 연결 관계를 표현
- 행렬의 (i, j)위치에 간선의 유무를 나타내며,
- 무방향 그래프의 경우 간선이 존재하면 1, 없으면 0 표현
- 방향 그래프는 i에서 j 방향의 간선이 존재하면 1, 없으면 0 표현
- 가중치 그래프는 간선이 존재하면 간선의 가중치, 없으면 0 표현
- 장점
- 단순한 구조로 구현이 쉽다
- O(1) 시간 복잡도로 간선의 존재 확인 가능하다
- 단점
- O(N^2)의 높은 공간 복잡도를 필요
class GraphAdjMatrix:
def __init__(self, vertices): # 그래프 정의
self.vertices = vertices
self.adj_matrix = [[0] * vertices for _ in range(vertices)]
def add_edge(self, src, dest): # 간선 추가
self.adj_matrix[src][dest] = 1
self.adj_matrix[dest][src] = 1
def remove_edge(self, src, dest): # 간선 제거
self.adj_matrix[src][dest] = 0
self.adj_matrix[dest][src] = 0
def is_edge(self, src, dest): # 노드 조회
return self.adj_matrix[src][dest] != 0인접 리스트 이용해서 그래프 만들기
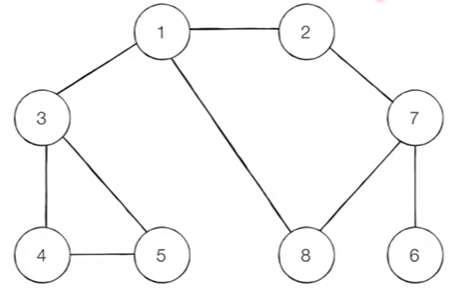
그래프(Graph)는 BFS나 DFS 및 최단경로를 구할 때 필수인 자료구조이다. 그래프를 만들줄 알아야 해당 문제들을 풀 수 있기 때문에 꼭 알아 두어야 한다. 위의 그림에서 노드1 ~ 노드 8까지 총 노드 8개와 노드들을 잇는 간선들로 이루어져 있다.
| node 1 | node 2 | node 3 | node 4 | node 5 | node 6 | node 7 | node 8 | |
| node 1 | 0 | 연결 | 연결 | X | X | X | X | 연결 |
| node 2 | 연결 | 0 | X | X | X | X | 연결 | X |
| node 3 | 연결 | X | 0 | 연결 | 연결 | X | X | X |
| node 4 | X | X | 연결 | 0 | 연결 | X | X | X |
| node 5 | X | X | 연결 | 연결 | 0 | X | X | X |
| node 6 | X | X | X | X | X | 0 | 연결 | X |
| node 7 | X | 연결 | X | X | X | 연결 | 0 | X |
| node 8 | 연결 | X | X | X | X | X | 연결 | 0 |
그래프를 만들기 위해서 일단 문제에서 주어진 그래프를 표로 바꾸는 것이 중요하다 위의 표에서 노드자신이 노드를 선택할 수 없으므로 대각선은 0으로 표현했고 , 노드가 연결되있으면 '연결', 그렇지 않으면 X로 표현하였다.

이제 만든 표를 바탕으로 그래프를 만들어 보자. 보통 2차원 배열로 그래프를 만드는데 위에서 부터 노드 1이고 마지막 배열에 담겨있는 정보가 노드 8이 연결되어 있는 노드들을 표현한 것이다. 그럴일은 거의 없겠지만 간선으로 연결된 노드가 아무것도 없는 노드는 [ ] 로 표현한다.
class GraphAdjList:
def __init__(self, vertices): # 그래프 크기 정의(vertice(node) 개수 입력)
self.vertices = vertices
self.adj_list = [[] for _ in range(vertices)]
def add_edge(self, src, dest): # 간선 추가
self.adj_list[src].append(dest)
self.adj_list[dest].append(src)
def remove_edge(self, src, dest): # 간선 제거
self.adj_list[src].remove(dest)
self.adj_list[dest].remove(dest)
def is_edge(self, src, dest): # 노드 조회
return dest in self.adj_list[src]- 장점
- 공간 효율성이 좋음
- 특정 정점의 인접 정점을 빠르게 찾을 수 있다
- 단점
- 두 정점 간의 간선 존재 확인을 위해 O(V) 의 시간 복잡도
dict()를 이용해서 그래프 만들기
이번엔 dictionary(딕셔너리)를 이용해서 그래프를 만들어 보려고 한다. dict() 함수를 호출해서 딕셔너리 객체를 만들어 준다음 각각의 노드가 어느 노드와 연결되 있는지 파악한다.
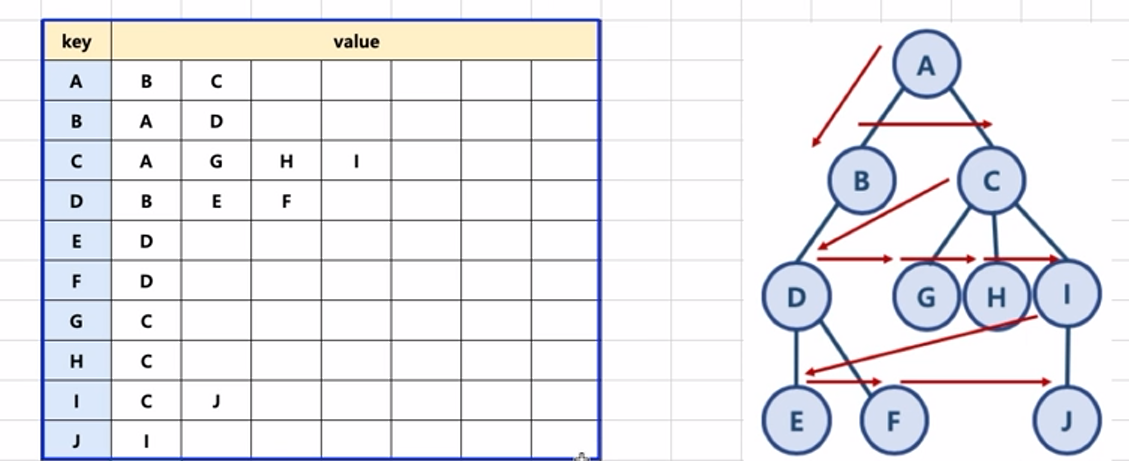
파악이 끝났다면 , 각각의 노드를 dict()를 이용해 표현해 준다.

그래프 순회

- 전위 순회(pre-order traversal) : 현재 노드 → 왼쪽 가지 → 오른쪽 가지
- 중위 순회(in-order traversal) : 왼쪽 가지 → 현재 노드 → 오른쪽 가지
- 후위 순회(post-order traversal) : 왼쪽 가지 → 오른쪽 가지 → 현재 노드
https://www.acmicpc.net/problem/1991
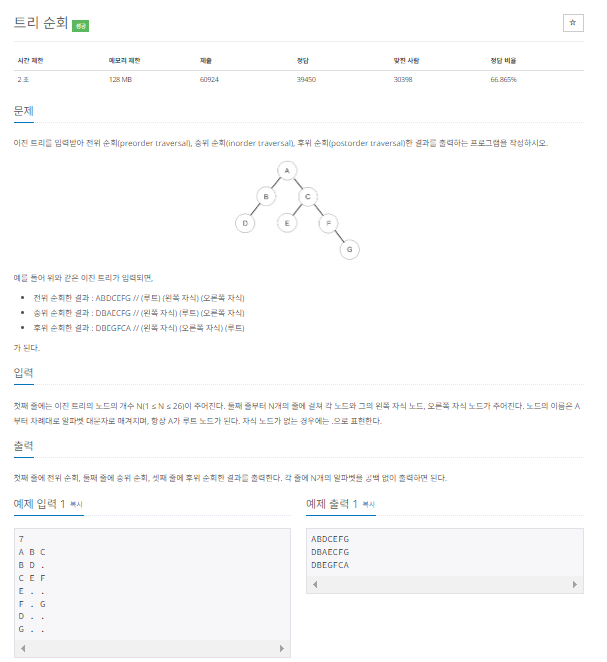
class Node :
def __init__(self,item,left,right) : # 간선 연결
self.item = item # 부모
self.left = left # 왼쪽
self.right = right # 오른쪽
# 부모노드가 '.' 값이 아니면 재귀를 통해 순회한다.
def preorder(node) : # 전위 순회(재귀 앞에 출력)
print(node.item,end="")
if node.left != '.' :
preorder(tree[node.left])
if node.right != '.' :
preorder(tree[node.right])
def inorder(node) : # 중위 순회(재귀 중간에 출력)
if node.left != '.' :
inorder(tree[node.left])
print(node.item, end="")
if node.right != '.' :
inorder(tree[node.right])
def postorder(node) : # 후위 순회(재귀 후에 출력)
if node.left != '.' :
postorder(tree[node.left])
if node.right != '.' :
postorder(tree[node.right])
print(node.item, end="")
n = int(input())
inputs = []
for _ in range(n):
inputs.append(input().split())
tree = {}
for item, left, right in inputs:
tree[item] = Node(item, left, right)
preorder(tree['A'])
print()
inorder(tree['A'])
print()
postorder(tree['A'])Tree

- 트리는 그래프의 일종의 순환성이 없는 무방향 그래프이다.
- 트리의 가장 바깥쪽 노드를 리프 노드(leaf node)라고 한다. 즉, 간선이 하나만 연결된 노드들이다. 또한 어떤 노드도 루트가 될 수 있다.
- 노드 개수와 간선 개수를 알면 다음 공식을 이용해서 트리 여부를 파악할 수 있다.(노드개수 = 간선개수 + 1)
- 구성 요소
- 루트 노트 : 계층 구조의 시작 노드
- 부모 자식 관계 : 트리의 모든 노드 간의 관계는 부모 자식 관계를 나타냄
- 리프 노드 : 자식 노드를 갖지 않는 노드
- 서브 트리 : 특정 노드와 그 노드의 자손 노드로 구성된 부분 그래프
- 트리의 표현
- 인접 행렬
- 인접 리스트
- 배열
- 배열을 이용하여 이진트리를 표현할 수 있다.
- 루트 노드는 배열의 첫 번째 요소에 저장
- 노드 i의 왼쪽 자식은 배열의 (2i + 1)번째 요소
- 노드 i의 오른쪽 자식은 배열의 (2i + 2)번째 요소 저장
class BinaryTree:
def __init__(self, size):
self.size = size
self.tree = [None] * size
# 루트 노드 값 설정
def set_root(self, value):
self.tree[0] = value
# 왼쪽 자식 값 설정
def set_left(self, parent_index, value):
left_index = 2 * parent_index + 1
if left_index < self.size:
self.tree[left_index] = value
else:
print("Index out of bounds for left child")
# 오른쪽 자식 값 설정
def set_right(self, parent_index, value):
right_index = 2 * parent_index + 2
if right_index < self.size:
self.tree[right_index] = value
else:
print("Index out of bounds for right child")
# 트리 인스턴스 생성
bt = BinaryTree(7)
bt.set_root(1)
bt.set_left(0, 2)
bt.set_right(0, 3)
bt.set_left(1, 4)
bt.set_right(1, 5)
bt.set_left(2, 6)
bt.set_right(2, 7)'computer science > Algorithm | Datastructure' 카테고리의 다른 글
| [Algorithm] 기초 수학 구현하기 (0) | 2023.05.17 |
|---|---|
| [python] 코딩테스트 skill (0) | 2023.05.16 |
| [자료구조] 스택(Stack) ,큐(Queue) , 우선순위 큐(Priority Queue) (0) | 2023.01.31 |
| [Algorithm] BFS(Breadth-First-Search), DFS(Depth-First-Search) (0) | 2022.11.25 |
| [Algorithm] greedy(탐욕법) (0) | 2022.11.18 |
Comments




